Clues and Strategies:
Let's walk through a puzzle together. These approaches are helpful tips to solve
Kenken. However, we don't recommend following these steps robotically. As you do
more and more of these puzzles, you'll soon realize that all these verbose explanations
are just momentary mind processes.
★☆★ There is more than one path to solve each puzzle. The path
below for this particular example includes the most helpful and common strategies
in the game, so don't worry if you can't understand all these at once. A working
solution is always good!
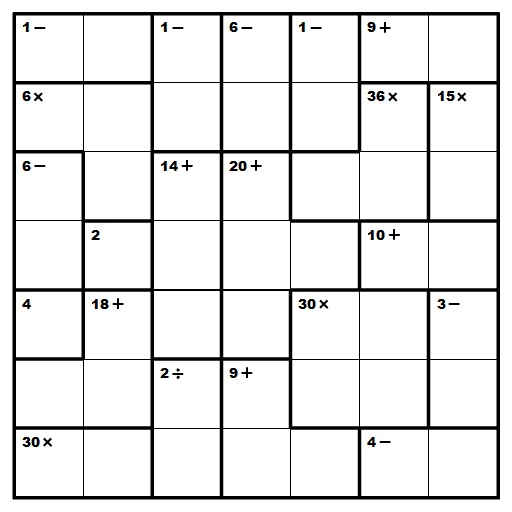
- First, fill in those squares that stand by themselves, so we have
this.
- Then look at the highlighted squares
here, because it's a 7-by-7 puzzle, the only possibility is 7 and 1. We don't
really need to worry about how the numbers fit in, but keep in mind that these squares
are "reserved".
- Now consider these. We have
couple combinations that work for this case:
1-6-1 or any order of 1-2-3. BUT, from 2. we learn that 1-6-1 won't work
since that will make two 1's in the first column. So they must be filled with 1,
2, and 3. And A-ha! We already have a 2 in the puzzle, therefore we arrive at this after some close analysis.
- Look for products that are multiples of 5. In particular,
these (the gray area is pretty difficult to attack on because it can be any
order of 1-2-3-5 and 1-6-1-5). We can easily make some notes to get
here.
***Similar approach can be done to those with a factor 7.
- Here's a tricky yet helpful part. The sum of each column is 28 (1+2+3+...+7), thus
the sum of the first two columns is 56 (28x2=56).
Right now, we know that the green, orange, and pink areas add up to 4, 8,
and 11, respectively (blue is 18 as given). Therefore, the bottom 12 squares in
these columns have a total of 49 (2 + 4
+ 8 + 2 + 4 +
18 + 11), which means
the top two squares have a sum 7. The two numbers also differ by 1, so they must
be 3 and 4, and because we have a 4 below, the grid looks like
this.
- With the 3, 4 we just filled in, the only possibility for the 9+ at the top
right must be 2-7 (or 7-2). And for the 4- at bottom right, it has to be
some order of 3 and 7 because 2-6 and 1-5 won't fit in that row.
Here is how the puzzle looks at this moment. Notice that 3 is "reserved"
in the right-most column? Quickly a few other digits can be
inserted.
- The only 3 numbers left in the right-most column are 1, 4, and 6. Only 1-4 satisfy
the 3-. We can easily fill in the 6 (and thus the 4 to its left) like
this.
- You may get stuck now, but contemplate on the last two blanks in the top row; they
are 5 and 6, and 6 goes with a 5 (Know why? Because 7 is already in the next row.)
It's a rare case, but this time 5 can't be above a 6. Otherwise, swapping those
two rectangles won't create any difference (Think closely and you'll realize why.),
which contradicts to the fact that there's exactly one final solution. So 5 pairs
with 4. (Apply the exact same analysis to the 18+ on the bottom left side
of the puzzle and you'll see where 7 goes into.) Now shift your focus to the 3rd
column from the left. The two squares on top add up to 11 (6+5) or 9 (5+4), the
middle three 14, making it a grand total of 25 or 23. The other two can only have
a sum of 3 or 5. But only the former case works; you have one number "x" and another
"2x", giving you a sum that is a multiple of 3. We can go back and label more squares.
- Continuing on the previous step, we can fill in the 3-5 on the far right and 1-3
in the second column, which leaves 6 in the last blank of the second row.
current look
- Use a similar procedure in step 5 and you'll find out
this and this (from step
8).
- There in that 36x, the two spots must be
6 on the left and 1 on the right (2-3 or 3-2 is impossible with the 3 in the
third row).
- Things start to fall into place. Using elimination or any other knowledge you have,
fill in the rest and you'll arrive at the
solution.
- If all attempts fail, it never harms to follow your instincts and make some guesses.
« Back to Kenken